List of indefinite integrals
Any of the above forumale can be verified by differentiating the right hand side. For example 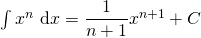 (
(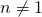 ) because
) because 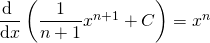 . This gives us a way to check our answers.
. This gives us a way to check our answers.
We can apply the rules from the list of indefinite integrals above to more complicated functions.
Two Useful Properties of Integrals
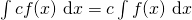
The integral of a constant times a function is equal to the constant times the integral of the function. Basically, this means that we can pull the constant out in front of the integral. This is similar to our constant multiple rule with derivatives.
2. 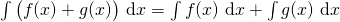
The integral of a sum of two functions is equal to the integral of the first function plus the integral of the second function. Basically, this means that the integral of the sum of two functions can be broken into two separate integrals for each function.
Examples.
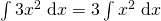 by property 1.
by property 1.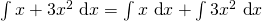 by property 2.
by property 2.
Examples Illustrating the Use of the Two Properties and the List of Indefinite Integrals
- Find
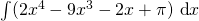 .
.
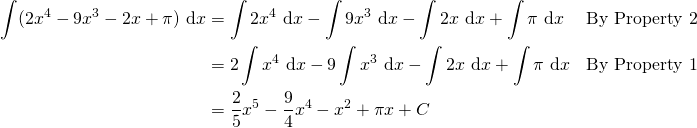
2. Evaluate 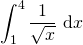 .
.
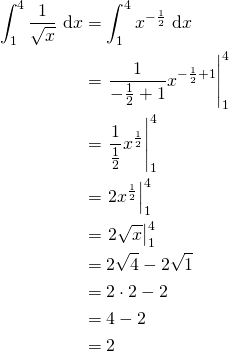
3. Find 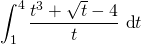 .
.
![Rendered by QuickLaTeX.com \begin{align*} \int_1^4 \frac{t^3 + \sqrt{t} - 4}{t} \, \d t &= \int_1^4 \left(t^2 + \frac{1}{\sqrt{t}} - \frac{4}{t}\right) \, \d t\\ &= \int_1^4 \left( t^2 + t^{-\frac12} - \frac{4}{t} \right) \, \d t\\ &= \left.\frac13 t^3 + 2 t^{\frac12} - 4 \ln t \right|_1^4\\ &= \frac13 (4)^3 + 2(4)^{\frac12} - 4 \ln 4 - \left[\frac13 (1)^3 + \underbrace{2(1)^{\frac12}}_2 - 4 \underbrace{\ln 1}_0 \right]\\ &= \frac{64}{3} + 4 - 4 \ln 2^2 - \frac13 - 2\\ &= \frac{64}{3} + 2 - 4 \ln 2^2 - \frac13 \\ &= \frac{63}{3} + \frac{6}{3} - 8 \ln 2\\ &= \frac{69}{3} - 8 \ln 2\\ &= 23 - 8 \ln 2 \end{align*}](https://kohar.ca/wp-content/ql-cache/quicklatex.com-ddef96f988afce14c9d5f7ff69a8106a_l3.png)

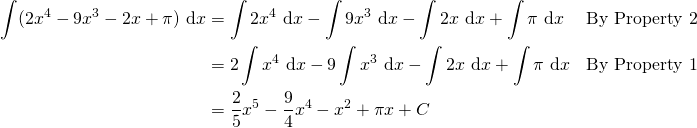
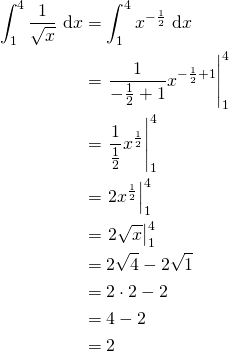
![Rendered by QuickLaTeX.com \begin{align*} \int_1^4 \frac{t^3 + \sqrt{t} - 4}{t} \, \d t &= \int_1^4 \left(t^2 + \frac{1}{\sqrt{t}} - \frac{4}{t}\right) \, \d t\\ &= \int_1^4 \left( t^2 + t^{-\frac12} - \frac{4}{t} \right) \, \d t\\ &= \left.\frac13 t^3 + 2 t^{\frac12} - 4 \ln t \right|_1^4\\ &= \frac13 (4)^3 + 2(4)^{\frac12} - 4 \ln 4 - \left[\frac13 (1)^3 + \underbrace{2(1)^{\frac12}}_2 - 4 \underbrace{\ln 1}_0 \right]\\ &= \frac{64}{3} + 4 - 4 \ln 2^2 - \frac13 - 2\\ &= \frac{64}{3} + 2 - 4 \ln 2^2 - \frac13 \\ &= \frac{63}{3} + \frac{6}{3} - 8 \ln 2\\ &= \frac{69}{3} - 8 \ln 2\\ &= 23 - 8 \ln 2 \end{align*}](https://kohar.ca/wp-content/ql-cache/quicklatex.com-ddef96f988afce14c9d5f7ff69a8106a_l3.png)
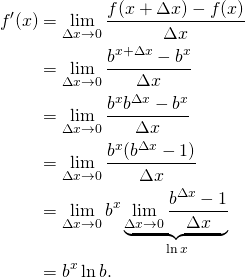
Recent Comments