We know that we have distributive rules that handle the disjunction and the conjunction, such as the following
![]()
But, does there exist a rule, for example, that would handle distributivity of the conjunction with the implication? In other words,
![]()
At least, the above case, the answer is no. We can see this by constructing a truth table like the one below; the truth values of ![]() are not the same as
are not the same as ![]() . Hence,
. Hence, ![]() and
and ![]() are not logically equivalent. Therefore, it’s not a rule that we can apply in our proofs.
are not logically equivalent. Therefore, it’s not a rule that we can apply in our proofs.
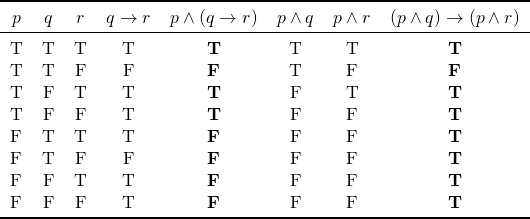
Tags: common mistakes, laws of logic, logic, rules of inference
No comments
Comments feed for this article
Trackback link: https://kohar.ca/mae-106-discrete-mathematics-with-probability-fall-2018/is-there-a-distributive-rule-for-the-implication/trackback/