Test 2: 31 October 2018
- You should know the following formulas.
- Combination
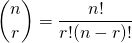 “
“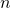 choose
choose  ” (order does not matter)
” (order does not matter) 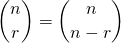 (The symmetry property) p. 167
(The symmetry property) p. 167- Permutation
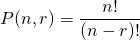 “
“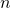 permute
permute  ” (order does matter)
” (order does matter)
- Combination
- Do the following exercises.
- 5.7.1 (a)–(h), 5.7.3, 5.7.4 (c)–(d), 5.7.5, 5.7.7, 5.7.9, 5.7.10, 5.7.11.
- 8.1, 5.8.3, 5.8.4, 5.8.5 (a, c, e, g, k), 5.8.7, 5.8.12, 5.8.13, 5.8.15, 5.8.17, 5.8.18, 5.2.20
- 5.11.1, 5.11.3, 5.11.4, 5.11.5, 5.11.6, 5.11.8, 5.11.15, 5.11.22, 5.11.24. Note that in 5.11.8, it should read “exactly 4 females?”
- Investigate Pascal’s triangle. Pascal’s triangle is a pattern that can be seen in Fig 7.8 on p. 280. There are many patterns that can be found in Pascal’s triangle. For example, the symmetry property can be seen in Fig. 7.9 on p. 283. The Fibonacci numbers (1, 1, 2, 3, 5, 8, 13, …), which is a sequence of numbers in which each number is the sum of the two preceding numbers, can also be found in Pascal’s triangle as seen in Fig. 7.10 on p. 283. The next couple of exercises will help you explore more patterns in Pascal’s triangle.
- 7.1.1, 7.1.2, 7.1.3, 7.1.4 (a, b, f) [Pascal’s Theorem 7.1.3]
- 7.1.12 (a, b, c, d, e). [The sum of entries in a row.] For part (c) iii:
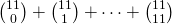 . For part (d): Generalize your findings to find an expression for the sum of row
. For part (d): Generalize your findings to find an expression for the sum of row 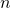 . In other words, what is the value of
. In other words, what is the value of 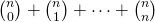 .
. - 7.1.13.
- 7.1.15 (a, b, c, d, e, f). [The sum of the squared entries in a row.]
- 7.1.17 (a, b, c, d). [The sum of the alternating sign entries in a row.]
- 7.1.18.
No comments
Comments feed for this article
Trackback link: https://kohar.ca/mae-106-discrete-mathematics-with-probability-fall-2018/mae-106-2018-assignment-7/trackback/