The quotient rule proof can be quite tedious if we are only allowed to use the definition of the derivative. In this post, this presents an alternative way of proving the quotient rule if we are allowed to use the product rule.
The Quotient Rule:
Let ![]() be the quotient of differentiable functions. Then, we can rearrange so that we have
be the quotient of differentiable functions. Then, we can rearrange so that we have
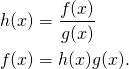
Assuming that ![]() is differentiable, we can use the product rule on
is differentiable, we can use the product rule on ![]() , which yields
, which yields
![]()
Then we isolate ![]() on one side of the equation.
on one side of the equation.
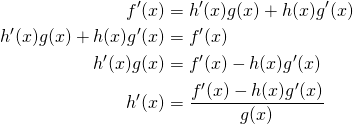
Now, we substitute ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} h'(x) &= \frac{f'(x) - h(x) g'(x)}{g(x)}\\ &= \frac{f'(x) - \frac{f(x)}{g(x)} g'(x)}{g(x)}\\ &= \frac{f'(x)}{g(x)} - \frac{f(x) g'(x)}{[g(x)]^2}\\ &= \frac{f'(x)}{g(x)}\cdot\frac{g(x)}{g(x)} - \frac{f(x) g'(x)}{[g(x)]^2}\\ &= \frac{f'(x) g(x)}{[g(x)]^2} - \frac{f(x) g'(x)}{[g(x)]^2}\\ &= \frac{f'(x) g(x) - f(x) g'(x)}{[g(x)]^2}\\ \end{align*}](https://kohar.ca/wp-content/ql-cache/quicklatex.com-d6924fc03ae74558598b0f0928fc05b6_l3.png)
We have arrived at the desired result, and this completes our proof.
No comments
Comments feed for this article
Trackback link: https://kohar.ca/mae-113-calculus-for-liberal-arts-winter-2018/a-second-more-elegant-proof-of-the-quotient-rule/trackback/