If
, then
.
Let ![]() . Using the definition of the derivative, we have
. Using the definition of the derivative, we have
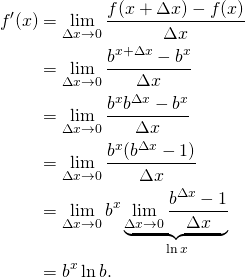
It would be nice if ![]() . Well, this occurs for a special value of
. Well, this occurs for a special value of ![]() ; we let
; we let ![]() .
.
This leads to the following:
If
, then
.
If
, then
.
Let ![]() . Using the definition of the derivative, we have
. Using the definition of the derivative, we have
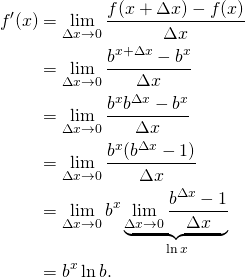
It would be nice if ![]() . Well, this occurs for a special value of
. Well, this occurs for a special value of ![]() ; we let
; we let ![]() .
.
This leads to the following:
If
, then
.
No comments
Comments feed for this article
Trackback link: https://kohar.ca/mae-113-calculus-for-liberal-arts-winter-2018/what-is-the-derivative-of-bx/trackback/