Here are some quick review videos for MAE 113.
Derivative Rules
Applications of the Derivative
- Finding the equation of the tangent to a curve
- Finding the global maximum value and global minimum value of a function
Solutions
Richard Kohar — Adventures into Mathematics
The course blog for MAE 113: Calculus for the Liberal Arts.
This course is intended to emphasize the basic concepts of Calculus: functions, limits, derivatives, and integrals.
The course syllabus can be found here: Course Syllabus.
Here are some quick review videos for MAE 113.
Derivative Rules
Applications of the Derivative
Solutions
Tags: Calculus, MAE 113, youtube, Youtube clip
I have posted assignment 8 here. The solutions for Section 11.3 are here. The solutions for Section 11.4 are here.
Tags: assignment, Calculus, MAE 113
Any of the above forumale can be verified by differentiating the right hand side. For example ![]() (
(![]() ) because
) because ![]() . This gives us a way to check our answers.
. This gives us a way to check our answers.
We can apply the rules from the list of indefinite integrals above to more complicated functions.
The integral of a constant times a function is equal to the constant times the integral of the function. Basically, this means that we can pull the constant out in front of the integral. This is similar to our constant multiple rule with derivatives.
2. ![]()
The integral of a sum of two functions is equal to the integral of the first function plus the integral of the second function. Basically, this means that the integral of the sum of two functions can be broken into two separate integrals for each function.
Examples.
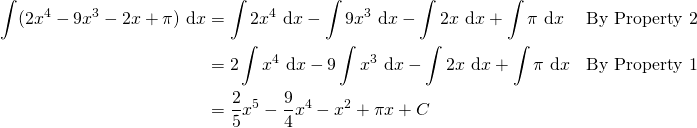
2. Evaluate ![]() .
.
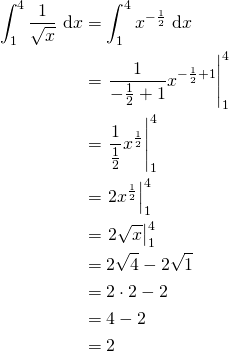
3. Find ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} \int_1^4 \frac{t^3 + \sqrt{t} - 4}{t} \, \d t &= \int_1^4 \left(t^2 + \frac{1}{\sqrt{t}} - \frac{4}{t}\right) \, \d t\\ &= \int_1^4 \left( t^2 + t^{-\frac12} - \frac{4}{t} \right) \, \d t\\ &= \left.\frac13 t^3 + 2 t^{\frac12} - 4 \ln t \right|_1^4\\ &= \frac13 (4)^3 + 2(4)^{\frac12} - 4 \ln 4 - \left[\frac13 (1)^3 + \underbrace{2(1)^{\frac12}}_2 - 4 \underbrace{\ln 1}_0 \right]\\ &= \frac{64}{3} + 4 - 4 \ln 2^2 - \frac13 - 2\\ &= \frac{64}{3} + 2 - 4 \ln 2^2 - \frac13 \\ &= \frac{63}{3} + \frac{6}{3} - 8 \ln 2\\ &= \frac{69}{3} - 8 \ln 2\\ &= 23 - 8 \ln 2 \end{align*}](https://kohar.ca/wp-content/ql-cache/quicklatex.com-ddef96f988afce14c9d5f7ff69a8106a_l3.png)
If
, then
.
Let ![]() . Using the definition of the derivative, we have
. Using the definition of the derivative, we have
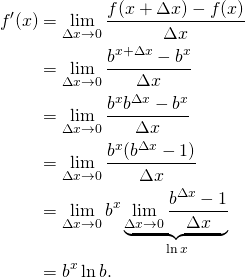
It would be nice if ![]() . Well, this occurs for a special value of
. Well, this occurs for a special value of ![]() ; we let
; we let ![]() .
.
This leads to the following:
If
, then
.
Assignment 6 has been handed out. You can find a copy of it here.
Also, assignment 7 has been handed out. You can find a copy of it here.
Each of these assignments refer to the handouts that I gave in class. If you do not have the handouts, please come see me.
Tags: assignment, Calculus, MAE 113
Do the questions from the large booklet that I handed out to you after the test.
You should have done Exercise 1 (all questions) already as instructed at the end of the test.
Exercise 2 (p. 352-3)
Exercise 3 (p. 354)
Tags: assignment, Calculus, homework, MAE 113
Assignment 5 is posted here. Solutions were handed out in class.
Tags: assignment, Calculus, MAE 113
The first test of MAE 113 will be on 13 February 2018.
No calculators, notes, or textbooks will be allowed.
You are responsible for all material
Tips:
This is a BBC video from 1986 on the development of calculus. For those that are interested in history, the presenter is looking at the original notes of Leibniz while he was developing calculus. He formalized the rules of differentiation within a 3 week timeframe.
Tags: BBC, Calculus, history, MAE 113, youtube, Youtube clip
The quotient rule proof can be quite tedious if we are only allowed to use the definition of the derivative. In this post, this presents an alternative way of proving the quotient rule if we are allowed to use the product rule.
The Quotient Rule:
Recent Comments