UPDATE: Our paper submitted to the IEEE Transactions on Neural Networks and Learning Systems has been published here.
You can read the pre-print paper here.
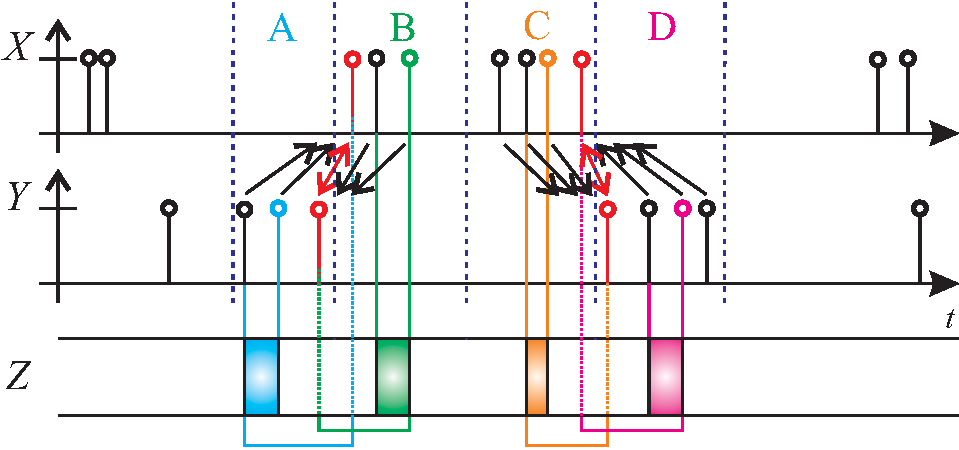
The LSTE events can be categorized into four groups: A, B, C, D. An event can be observed (X) or predicted (Y), and is mapped to its closest neighbor (in red) in the other stream, which can either come before or after. The rectangles in Z represent the window of input signals (in Z) observed for a given event (in X) or prediction (in Y).
In this paper, we propose a new error cost function based on the squared timing error (STE) that can be used for binary time series prediction. Learning on-line to predict the timing of events is important in many domains (e.g., finance, medicine, music, and robotics). However, machine learning algorithms are not efficient at solving this problem and in particular, cannot do this successfully on-line. We show that STE is better than sum-squared error (SSE) and dynamic time warping (DTW) for these kinds of problems by providing more information about the timing error. In particular, we show that STE can be used to train a type of recurrent neural network (in fact, we train an LSTM) by providing a direct gradient about the amount of time-shift and time-warping, which is not conveyed by SSE. In contrast with DTW, STE requires only local temporal information.
It will, in our opinion, generate great interest in on-line learning algorithms for time series prediction.
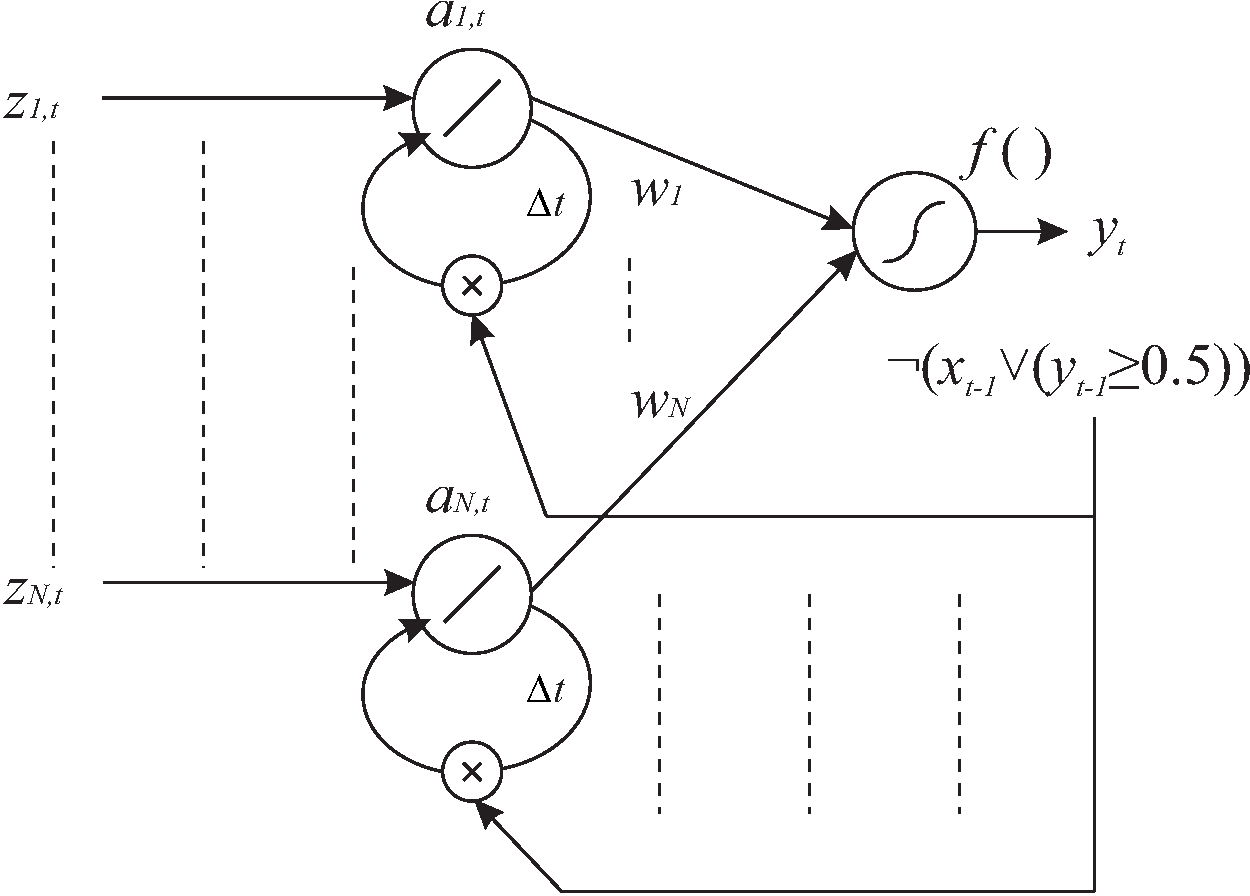
The LSTE prediction system seen as a special LSTM network.
Test 2: 31 October 2018
- You should know the following formulas.
- Combination
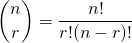 “
“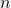 choose
choose  ” (order does not matter)
” (order does not matter) 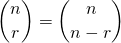 (The symmetry property) p. 167
(The symmetry property) p. 167- Permutation
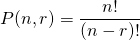 “
“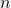 permute
permute  ” (order does matter)
” (order does matter)
- Combination
- Do the following exercises.
- 5.7.1 (a)–(h), 5.7.3, 5.7.4 (c)–(d), 5.7.5, 5.7.7, 5.7.9, 5.7.10, 5.7.11.
- 8.1, 5.8.3, 5.8.4, 5.8.5 (a, c, e, g, k), 5.8.7, 5.8.12, 5.8.13, 5.8.15, 5.8.17, 5.8.18, 5.2.20
- 5.11.1, 5.11.3, 5.11.4, 5.11.5, 5.11.6, 5.11.8, 5.11.15, 5.11.22, 5.11.24. Note that in 5.11.8, it should read “exactly 4 females?”
- Investigate Pascal’s triangle. Pascal’s triangle is a pattern that can be seen in Fig 7.8 on p. 280. There are many patterns that can be found in Pascal’s triangle. For example, the symmetry property can be seen in Fig. 7.9 on p. 283. The Fibonacci numbers (1, 1, 2, 3, 5, 8, 13, …), which is a sequence of numbers in which each number is the sum of the two preceding numbers, can also be found in Pascal’s triangle as seen in Fig. 7.10 on p. 283. The next couple of exercises will help you explore more patterns in Pascal’s triangle.
- 7.1.1, 7.1.2, 7.1.3, 7.1.4 (a, b, f) [Pascal’s Theorem 7.1.3]
- 7.1.12 (a, b, c, d, e). [The sum of entries in a row.] For part (c) iii:
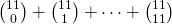 . For part (d): Generalize your findings to find an expression for the sum of row
. For part (d): Generalize your findings to find an expression for the sum of row 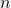 . In other words, what is the value of
. In other words, what is the value of 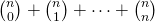 .
. - 7.1.13.
- 7.1.15 (a, b, c, d, e, f). [The sum of the squared entries in a row.]
- 7.1.17 (a, b, c, d). [The sum of the alternating sign entries in a row.]
- 7.1.18.
We know that we have distributive rules that handle the disjunction and the conjunction, such as the following
![]()
But, does there exist a rule, for example, that would handle distributivity of the conjunction with the implication? In other words,
![]()
At least, the above case, the answer is no. We can see this by constructing a truth table like the one below; the truth values of ![]() are not the same as
are not the same as ![]() . Hence,
. Hence, ![]() and
and ![]() are not logically equivalent. Therefore, it’s not a rule that we can apply in our proofs.
are not logically equivalent. Therefore, it’s not a rule that we can apply in our proofs.
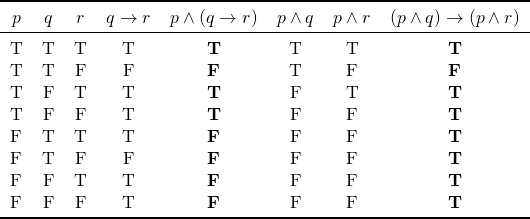
Tags: common mistakes, laws of logic, logic, rules of inference
Quiz: 24 October 2018
- Do the following exercises.
- Kohar 5.2.2, 5.2.3, 5.2.8, 5.2.10, 5.2.16, 5.2.18, 5.2.22, 5.2.23, 5.2.24, 5.2.25
- Kohar 5.3.1, 5.3.2, 5.3.3, 5.3.5, 5.3.6, 5.3.7
- Kohar 5.4.1, 5.4.2 (a)–(b), 5.4.3, 5.4.5, 5.4.9, 5.4.10, 5.4.12
- Kohar 5.5.1
- Kohar 5.6.2, 5.6.3, 5.6.4
- The members of Kingston City Council are to vote either yes or no (but not both) on each of seven issues. In marking a ballot, each councilor has the option of abstaining on as many as six of the issues, but cannot abstain on all seven issues. In how many ways can a ballot be marked? [Ans: 2186]
- Draw the Venn diagram for three sets
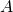 ,
, 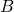 , and
, and 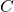 that are mutually exclusive.
that are mutually exclusive. - Determine whether the following statements are true or false. Use a Venn diagram to aid you in answering.
- If
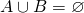 , then
, then 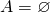 , and
, and 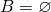 .
. 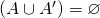
- If
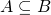 , then
, then 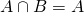 .
. - If
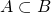 and
and  , then
, then 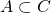 .
. - If all cadets are students, and all students are academics, then all cadets are academics.
- If
- Kohar 3.4.3, 3.4.5, 3.4.6, 3.4.9, 3.4.10, 3.4.11, 3.4.12, 3.4.13, 3.7.3.
- Kohar 3.5.3, 3.5.4
- Using the rules of set algebra show the following:
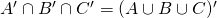
- Exercises 3.1.1, 3.1.2, 3.1.3, 3.1.5, 3.1.6, 3.1.8
- Exercises 3.3.1, 3.3.3, 3.3.4, 3.3.5, 3.3.7, 3.3.8, 3.3.10, 3.3.11
- Exercises 3.7.4
- Create Venn diagrams for the following sets:
-
-
- Know the following definitions.
- Argument (what constitutes a valid argument?)
- Fallacy
- Modus ponens
- Modus tollens
- Do the following exercises from the textbook (Kohar).
- 2.2.3 (a), (b), 2.2.4, 2.2.5, 2.2.6, 2.2.7, 2.2.8, 2.2.9, 2.2.12, 2.2.13, 2.2.14, 2.2.15, 2.2.16, 2.2.17, 2.2.19
- 2.4.1, 2.4.2
- 2.9.4 a) b) c), 2.9.5, 2.9.6, 2.9.7
- Using the rules of inference, prove that modus ponens is a valid argument; that is, show that
![Rendered by QuickLaTeX.com [(p\to q)\wedge p]\to q\Leftrightarrow \mathbb{T}](http://kohar.ca/wp-content/ql-cache/quicklatex.com-5ecbb96ae6a0e095dd30422e266d0068_l3.png) .
. - The following argument is called affirming the consequent. Is it valid?
- Know the following definitions.
(Premise)
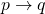
(Premise)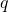
(Conclusion)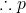
-
- The following argument is called denying the antecedent. Is it valid?
(Premise)
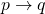
(Premise)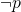
(Premise)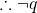
-
Class will begin earlier than usual at 9:30 am. The quiz will start at this time.
Quiz: 19 September 2018 (at the beginning of class)
Do the following exercises from the textbook (Kohar).
- 1.4.2
- 1.6.2, 1.6.4
- 1.7.1, 1.7.3, 1.7.4 (c), 1.7.5, 1.7.6, 1.7.7, 1.7.8, 1.7.9, 1.7.10, 1.7.12, 1.7.16
- 1.8.6
- 2.2.3 (a), (b), 2.2.4, 2.2.5, 2.2.6, 2.2.7, 2.2.8, 2.2.9, 2.2.14, 2.2.15, 2.2.17, 2.2.19
Recent Comments