UPDATE: Our paper submitted to the IEEE Transactions on Neural Networks and Learning Systems has been published here.

You can read the pre-print paper here.

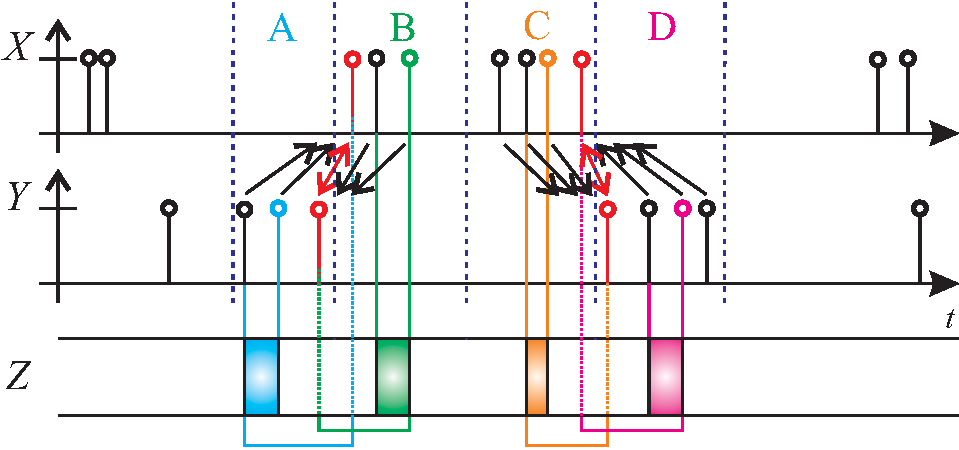
The LSTE events can be categorized into four groups: A, B, C, D. An event can be observed (X) or predicted (Y), and is mapped to its closest neighbor (in red) in the other stream, which can either come before or after. The rectangles in Z represent the window of input signals (in Z) observed for a given event (in X) or prediction (in Y).

In this paper, we propose a new error cost function based on the squared timing error (STE) that can be used for binary time series prediction. Learning on-line to predict the timing of events is important in many domains (e.g., finance, medicine, music, and robotics). However, machine learning algorithms are not efficient at solving this problem and in particular, cannot do this successfully on-line. We show that STE is better than sum-squared error (SSE) and dynamic time warping (DTW) for these kinds of problems by providing more information about the timing error. In particular, we show that STE can be used to train a type of recurrent neural network (in fact, we train an LSTM) by providing a direct gradient about the amount of time-shift and time-warping, which is not conveyed by SSE. In contrast with DTW, STE requires only local temporal information.

It will, in our opinion, generate great interest in on-line learning algorithms for time series prediction.

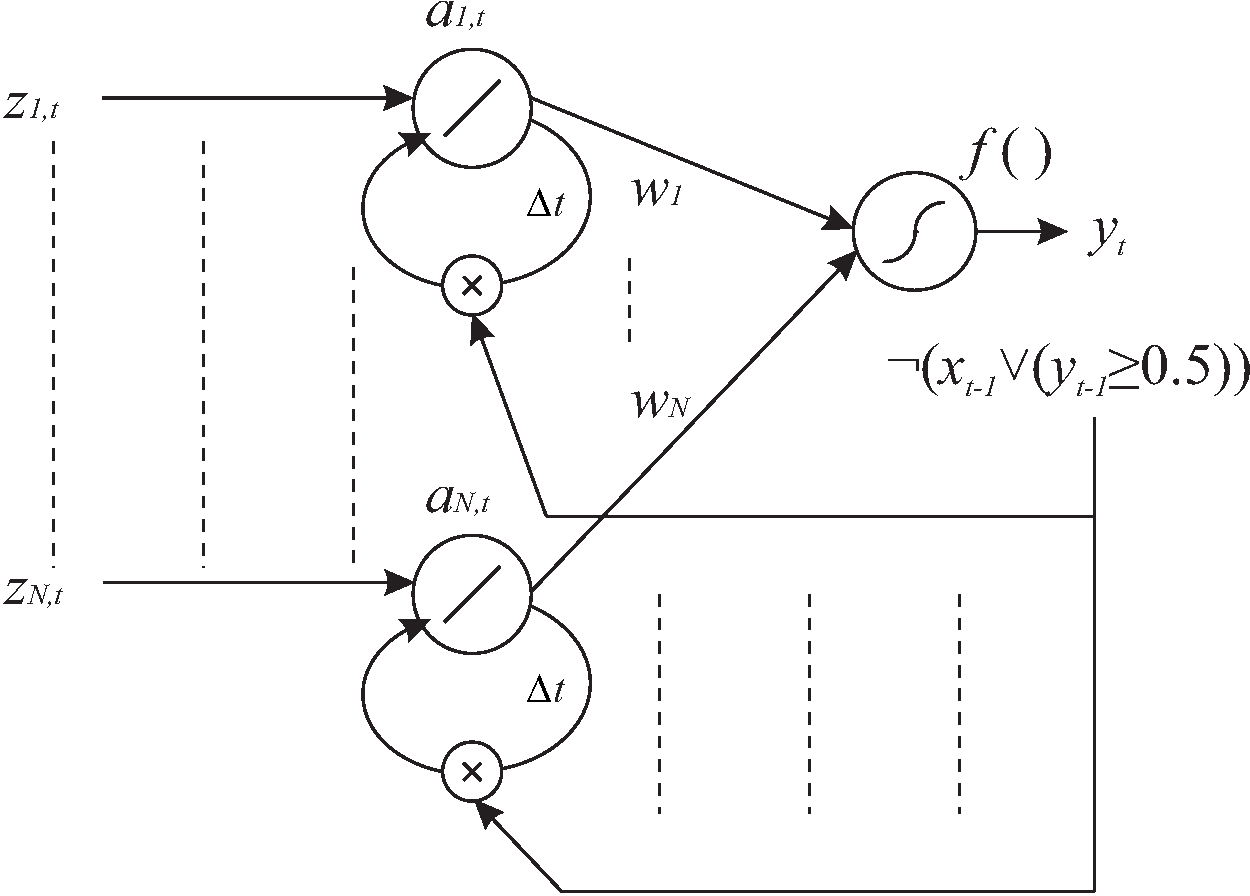
The LSTE prediction system seen as a special LSTM network.