Informally, a function represents how one quantity depends on another. Functions can be used as mathematical models of real-world data such as showing how much interest has accrued in a savings account depends on the amount time elapsed since the principal was deposited.

Functions can be expressed verbally (describing the relationship between the quantities in words), numerically (with the use of a table of values), algebraically (using a formula), and visually (with the use of a graph).

A function is a mapping that assigns to each element in a set (called the domain), one and only one element in a set (called the range).

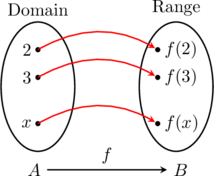
Let be a function, and if is a number in the domain of , then the number onto which maps is denoted by . We read as “ at .”

A function maps each element of its domain onto only one element of its range. Graphically, this means that there is only one value of that can correspond to any value of .

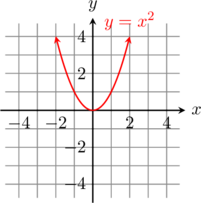
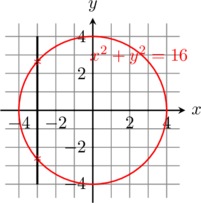
Vertical line test for a function: Any vertical line intersects the graph of a function in at most one point.

For example, a parabola would pass the vertical line test; hence it is a function.

But, a circle does not pass the vertical line test; hence, it is not a function.